Question

G(x)= f (1/4 • x) = (1/4 • x) 1/2

Answer 1

The value of
`\(h'(1) = 6\)`.

To find
`\(h'(1)\)`, the derivative of
`\(h(x)\)` at x = 1, we can use the quotient rule. The quotient rule states that if
`\(h(x) = (f(x))/(g(x))\), then \(h'(x) = (f'(x)g(x) - f(x)g'(x))/((g(x))^2)\).`

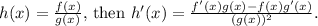
In this case,
`\(h(x) = (f(x)g(x))/(f(x) - g(x))\)`. Let's find
`\(h'(x)\)` and then evaluate it at x = 1:

`\[ h'(x) = ((f'(x)g(x) + f(x)g'(x))(f(x) - g(x)) - (f(x)g(x))(f'(x) - g'(x)))/((f(x) - g(x))^2) \]`

Now, plug in the given values and simplify:

`\[ h'(1) = ((-6 \cdot (-4) + 4 \cdot 2)(4 - (-4)) - (4 \cdot (-4))( -6 - 2))/((4 - (-4))^2) \]`

`\[ h'(1) = ((24 + 8)(8) - (-16)(-8))/((8)^2) \]`

`\[ h'(1) = (32 \cdot 8 + 128)/(64) \]`

`\[ h'(1) = (256 + 128)/(64) \]`

`\[ h'(1) = (384)/(64) \]`

`\[ h'(1) = 6 \]`

Therefore,
`\(h'(1) = 6\)`.

Complete question:

Suppose that f and g are function that are differentiable at x = 1 and that f(1) = 4, f'(1) = -6, g(1) = -4, and g'(1) = 2. Find h'(1). h(x) = f(x)g(x)/f(x) - g(x) h'(1) = 1