For
 , plotted points include (0, 0), (-1, -0.5), (-2, -4), (1, -0.5), and (2, -4), representing key values for x, demonstrating the function's behavior on a graph.
, plotted points include (0, 0), (-1, -0.5), (-2, -4), (1, -0.5), and (2, -4), representing key values for x, demonstrating the function's behavior on a graph.
Given the function
 let's find the corresponding
let's find the corresponding
 values for various
values for various
 values:
values:
When
 :
:
![\[y = -(1)/(2) * 0^3 = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yi9mepkoxc4yskl73434wrbva5i4dm6h97.png)
So, the point is (0, 0).
For negative
 values:
values:
When
 :
:
![\[y = -(1)/(2) * (-1)^3 = -(1)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zpulcxt0jdaacd7dp7s5orezeca173dkng.png)
The point is (-1, -0.5).
When

![\[y = -(1)/(2) * (-2)^3 = -4\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wr9brhrurfy4ymgqx52newjwugc4qw9j3e.png)
The point is (-2, -4).
For positive
 -values:
-values:
When \(x = 1\):
![\[y = -(1)/(2) * 1^3 = -(1)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vy7n6fn64uk9mpmrab1e2ai1rcz8oal4jt.png)
The point is (1, -0.5).
When
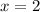 :
:
![\[y = -(1)/(2) * 2^3 = -4\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bb7zi227mpwp2gximtcl89b67fgh1fi9ar.png)
The point is (2, -4).
Plotting these points on a graph gives a visual representation of the function
 .
.