Question

A 100.0g sample of water at 90 degree C is added to a 500.0g sample of water at 10 degree C what is the final temperature of water ?

Answer 1

To find the final temperature, you can use the principle of conservation of energy, which states that the heat lost by the hot water equals the heat gained by the cold water. The final temperature of water is 23.32°C.

Step-by-step explanation:

To find the final temperature, you can use the principle of conservation of energy, which states that the heat lost by the hot water equals the heat gained by the cold water. The formula for this principle is:

`Q_{\text{hot}} = Q_{\text{cold}}`

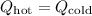
The heat gained or lost by a substance is given by the formula:

Q = m · c · ΔT

where m is the mass, c is the specific heat, and ΔT is the change in temperature.

For the hot water:

`\[ Q_{\text{hot}} = m_{\text{hot}}c_{\text{water}}\Delta T_{\text{hot}} \]`

For the cold water:

`\[ Q_{\text{cold}} = m_{\text{cold}}c_{\text{water}}\Delta T_{\text{cold}} \]`

Since the final temperature will be the same for both substances, you can set up an equation:

`\[ m_{\text{hot}}c_{\text{water}}\Delta T_{\text{hot}} = m_{\text{cold}}c_{\text{water}}\Delta T_{\text{cold}} \]`

Now plug in the values:

`\[ (m_{\text{hot}}c_{\text{water}}\Delta T_{\text{hot}})_{\text{initial}} = (m_{\text{cold}}c_{\text{water}}\Delta T_{\text{cold}})_{\text{initial}} \]`

`\[ m_{\text{hot}}c_{\text{water}}(T_{\text{hot}} - T_{\text{final}}) = m_{\text{cold}}c_{\text{water}}(T_{\text{final}} - T_{\text{cold}}) \]`

Now, solve for
`\( T_{\text{final}} \)`:

`\[ T_{\text{final}} = \frac{m_{\text{hot}}c_{\text{water}}T_{\text{hot}} + m_{\text{cold}}c_{\text{water}}T_{\text{cold}}}{m_{\text{hot}}c_{\text{water}} + m_{\text{cold}}c_{\text{water}}} \]`

Now plug in the values:

`\[ T_{\text{final}} = \frac{(100.0 \, \text{g})(4.18 \, \text{J/g}^\circ \text{C})(90^\circ \text{C}) + (500.0 \, \text{g})(4.18 \, \text{J/g}^\circ \text{C})(10^\circ \text{C})}{(100.0 \, \text{g})(4.18 \, \text{J/g}^\circ \text{C}) + (500.0 \, \text{g})(4.18 \, \text{J/g}^\circ \text{C})} \]`

`\[ T_{\text{final}} = ((37620+20900))/((418+2090)) \]`

`\[ T_{\text{final}} = (58520)/(2508) \]`

`\( T_{\text{final}} \)` = 23.32 °C

So, the final temperature of water is 23.32°C.