In a square PSRQ, the diagonals PR and SQ intersect at the midpoint O. You've mentioned that PO = 3. Since PO is the midpoint of PR, RO is also 3.
Now, using the Pythagorean Theorem in right triangle ROQ, we can find the length of RQ.
![\[ RQ^2 = RO^2 + OQ^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nazb2hdd2otvr5cxog212sq1mcmv4kmpb5.png)
Substitute the given values:
![\[ RQ^2 = 3^2 + 3^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dg4ta1cfo8tohwctn554aen472p3fbi35j.png)
![\[ RQ^2 = 9 + 9 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ta7vveapyyv2j22or1xu9rc2yqgew5a27g.png)
![\[ RQ^2 = 18 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gqtqhi9tjfzrntz684gs1dj0oru296mjeu.png)
![\[ RQ = √(18) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pusxncy49f2c8qldr2qpbgh6hfau606ubg.png)
Rounding to the nearest tenth,
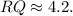
Therefore, the correct value for QR is approximately 4.2.