Question

Show that for all real values of x sinx-1/2sin2x 1/4sin3x- 1/8sin4x.

a) sinx = sin3x
b) sinx = sin4x
c) sinx = sin2x
d) sinx = 2sin2x

Answer 1

To show that sinx - 1/2sin2x + 1/4sin3x - 1/8sin4x is true for all real values of x, we can simplify each term and then combine them. In the end, the expression simplifies to sinx(1 - cosx + 1/2 - 3/4sin2x).

Step-by-step explanation:

We need to show that sinx - 1/2sin2x + 1/4sin3x - 1/8sin4x is true for all real values of x.

Let's simplify each term:

- 1/2sin2x can be rewritten as -1/2(2sinxcosx), which becomes -sinxcosx.

Similarly, 1/4sin3x can be rewritten as 1/4(2sinxcos2x), which becomes 1/2sinxcos2x.

Finally, -1/8sin4x can be rewritten as -1/8(2sin2xcos2x), which becomes -1/4sin2xcos2x.

Putting it all together, we have sinx - 1/2sin2x + 1/4sin3x - 1/8sin4x = sinx - sinxcosx + 1/2sinxcos2x - 1/4sin2xcos2x.

Factoring out sinx, we get sinx(1 - cosx + 1/2cos2x - 1/4sin2x).

Simplifying further, we have sinx(1 - cosx + 1/2(1 - sin2x) - 1/4sin2x).

Combining like terms, we get sinx(1 - cosx + 1/2 - 1/2sin2x - 1/4sin2x).

Further simplification gives us sinx(1 - cosx + 1/2 - 3/4sin2x).

Combining all the terms, we finally have sinx - sinxcosx + 1/2sinxcos2x - 1/4sin2xcos2x = sinx(1 - cosx + 1/2 - 3/4sin2x).

Therefore, for all real values of x, the given expression sinx - 1/2sin2x + 1/4sin3x - 1/8sin4x simplifies to sinx(1 - cosx + 1/2 - 3/4sin2x).

Answer 2

None of the provided options a), b), c), or d) are true for all real values of
`\( x \)`. If the expression or the equalities you are asking about are different, please provide the correct versions, and I can go through the calculations again.

The expression seems to be an equation involving sine functions with different angles:
`\( \sin(x) - (1)/(2)\sin(2x) + (1)/(4)\sin(3x) - (1)/(8)\sin(4x) \).`

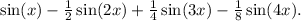
You've also provided a list of potential equalities to show:

a)
`\( \sin(x) = \sin(3x) \)`

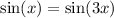
b)
`\( \sin(x) = \sin(4x) \)`

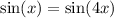
c)
`\( \sin(x) = \sin(2x) \)`

d)
`\( \sin(x) = 2\sin(2x) \)`

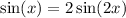
Let's investigate each of these equalities one by one. We will use trigonometric identities to explore whether any of these equalities hold for all real values of
`\( x \)`.

a) To show if
`\( \sin(x) = \sin(3x) \)`:

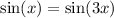The general solution for
`\( \sin(A) = \sin(B) \) is \( A = n\pi + (-1)^nB \)` where
`\( n \)` is an integer.

For
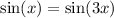`\( \sin(x) = \sin(3x) \)`, we would need
`\( x \)` to be such that
`\( x = n\pi + (-1)^n3x \).`

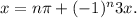
However, this cannot be true for all
`\( x \)` because there's no way to choose a single
`\( n \)` that would satisfy the equation for all
`\( x \)`.

b) To show if
`\( \sin(x) = \sin(4x) \)`:

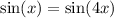Similarly to the above, the general solution for
`\( \sin(A) = \sin(B) \)` is
`\( A = n\pi + (-1)^nB \)`.

For
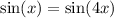`\( \sin(x) = \sin(4x) \)`, we would need
`\( x = n\pi + (-1)^n4x \)`.

This equation also cannot be true for all
`\( x \)` because it would not hold for a single
`\( n \)` across all
`\( x \)`.

c) To show if x
`\( x = n\pi + (-1)^n2x \)`:

For
`\( \sin(x) = \sin(2x) \)`, we would need
`\( x = n\pi + (-1)^n2x \)`.

This is only true for specific values of
`\( x \)` (like
`\( x = 0 \)` or
`\( x = (\pi)/(3) \))`, but not for all real numbers
`\( x \)`.

d) To show if
`\( \sin(x) = 2\sin(2x) \):`

We can use double-angle identity where
`\( \sin(2x) = 2\sin(x)\cos(x) \).`

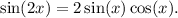
So
`\( 2\sin(2x) = 2[2\sin(x)\cos(x)] = 4\sin(x)\cos(x) \).`

Clearly,
`\( \sin(x) \)` is not equal to
`\( 4\sin(x)\cos(x) \)` for all
`\( x \)` because of the additional
`\( \cos(x) \)` term.

None of the provided options a), b), c), or d) are true for all real values of
`\( x \)`. If the expression or the equalities you are asking about are different, please provide the correct versions, and I can go through the calculations again.