a) The operator's efficiency function is
 after working 2 hours.
after working 2 hours.
b) After 3 hours, efficiency is 72%, and after 5 hours, efficiency is 58%, derived from the calculated function.
a) Find E(t), given that the operator's efficiency after working 2 hr is 67% (E(2) = 67):
Given the differential equation
 , we need to solve it to find
, we need to solve it to find
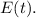
![\[ \int dE = \int (25 - 8t)dt \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ngd9o8dvtrwk5qkgawanrd5dbpnopl62b0.png)
Integrating both sides:
![\[ E(t) = \int (25 - 8t)dt \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6plih5n2jx4khezrubq66lb09bd22pgyvb.png)
\[ E(t) = 25t - 4t^2 + C \]
Now, use the given condition E(2) = 67 to solve for C:
![\[ E(2) = 25(2) - 4(2)^2 + C = 67 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/blmo5bpzvr7ciyj6i30imr22m4zpulsku2.png)
50 - 16 + C = 67
C = 33
So, the operator's efficiency function is
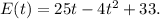
b) Use the answer in part (a) to find the operator's efficiency after 3 hr and after 5 hr:
![\[ E(3) = 25(3) - 4(3)^2 + 33 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qk5hozkiue69y7nwajvcej0pg181euelfu.png)
E(3) = 75 - 36 + 33
E(3) = 72
After 3 hours, the operator's efficiency is 72%.
![\[ E(5) = 25(5) - 4(5)^2 + 33 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qfl85kcxablxhzatrxpmpu1by4up0frrkv.png)
E(5) = 125 - 100 + 33
E(5) = 58
After 5 hours, the operator's efficiency is 58%.
The probable question may be:
The rate at which a machine operator's efficiency, E (expressed as a percentage), changes with respect to time t is given by dE/dt= 25-8t, where t is the number of hours the operator has been at work. a) Find E(t), given that the operator's efficiency after working 2 hr is 67%; that is, E(2)=67. b) Use the answer in part (a) to find the operator's efficiency after 3 hr; after 5 hr.