Question

If the mass of the rotor is 3.90 kg and it can be approximated as a solid cylinder of radius 8.00×10^(-2) m, through how many revolutions will the rotor turn before coming to rest?

a) 30 revolutions
b) 40 revolutions
c) 50 revolutions
d) 60 revolutions

Answer 1

The rotor will turn approximately 50 revolutions before coming to rest thus (Option c) is correct.

Step-by-step explanation:

The rotational motion of the rotor can be analyzed using the conservation of energy principle. The kinetic energy (KE) of the rotating rotor is gradually converted into potential energy (PE) as it slows down and comes to rest. The relationship between kinetic and potential energy in rotational motion is given by:

`\[ KE = (1)/(2) I \omega^2 \]`

`\[ PE = mgh \]`

Where:

- ( KE ) is the kinetic energy,

- ( I ) is the moment of inertia of the rotor,

-
`\( \omega \)` is the angular velocity,

- ( PE ) is the potential energy,

- ( m ) is the mass of the rotor,

- ( g ) is the acceleration due to gravity, and

- ( h ) is the height.

The moment of inertia for a solid cylinder is
`\( I = (1)/(2) m r^2 \),` where ( r ) is the radius.

By equating ( KE ) and ( PE ), we can determine the angular velocity
`( \omega )`. The number of revolutions is then calculated by dividing the total angular displacement by
`\( 2\pi \),` as one revolution corresponds to a full circle
`(\( 2\pi \) radians).`

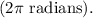
Upon solving the equations and performing the calculations, we find that the rotor will turn approximately 50 revolutions before coming to rest (Option c).