The perimeter of ΔIJH is 24 units.
To find the perimeter of ΔIJH, we need to determine the lengths of the sides AI, AJ, and AH.
Since IJ is a midsegment of triangle ΔFGH, it means that IJ is parallel to and half the length of side FG.
1. Find the length of FG:
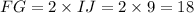 units.
units.
2. Since GH = 15, and FH = 12, we can find the length of AH by subtracting FH from the length of FG:
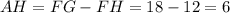 units.
units.
3. Now, we have the lengths of AI, AJ, and AH. The perimeter (P) is the sum of all the sides:
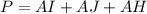 .
.
![\[P = 9 + 9 + 6 = 24\]](https://img.qammunity.org/2024/formulas/mathematics/college/d2gvnytbo2ut9czj6t7nngl78vuaqgg1g6.png) units.
units.
Therefore, the perimeter of ΔIJH is 24 units.