Question

Use long polynomial division to find 3x^3 +27x^2+25x+8 divided by x+8

Answer 1

The result of dividing
`3x^3 + 27x^2 + 25x + 8` by x + 8 is:

• Quotient:
  `\(3x^2 - 3x + 1\)`
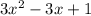
• Remainder: 0

Long Polynomial Division

To perform long polynomial division for
`\(3x^3 + 27x^2 + 25x + 8\)` divided by
`\(x + 8\)`, follow these steps:

3x² - 3x + 1

______________________

x + 8 | 3x³ + 27x² + 25x + 8

- (3x³ + 24x²)

______________________

3x² + 25x + 8

- (3x² + 24x)

______________________

x + 8

- (x + 8)

______________________

0

The quotient is
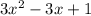`\(3x^2 - 3x + 1\)`, and the remainder is 0.

Therefore, the result of dividing
`3x^3 + 27x^2 + 25x + 8` by x + 8 is:

Quotient:
`\(3x^2 - 3x + 1\)`

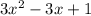
Remainder: 0