Question

How to write the radical expression for the 8th square root of x?

A. x^(1/8)
B. x^(1/4)
C. x^(1/16)
D. x^(1/2)

Answer 1

The radical expression for the 8th square root of x is represented as
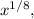`\(x^(1/8)\),` which corresponds to option A.

Step-by-step explanation:

The radical expression for the 8th square root of x signifies finding a value which, when raised to the power of 8, yields x. Mathematically, this is expressed as
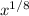`\(x^(1/8)\)`. The numerator in the exponent, 1, indicates that it's the 8th root, while the denominator, 8, signifies the root's degree. In this scenario, raising xto the power of 1/8 returns the value that, when multiplied by itself 8 times, results in x. Therefore, the correct choice among the options presented is
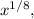`\(x^(1/8)\),` aligning with option A.

Understanding radical expressions is fundamental in mathematics, especially when dealing with roots and exponents. The notation
`\(x^(1/n)\)`represents the nth root of x, where n is the root's degree. In this specific case, the 8th square root of x involves finding a value that, when raised to the power of 8, equals x. Therefore,
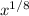`\(x^(1/8)\)` is the suitable radical expression for the 8th square root of x. This expression simplifies the understanding and manipulation of complex radical expressions and aids in various mathematical calculations and problem-solving situations.