Question

To save money for her son's college tuition, Christine invests every month in an annuity that pays interest, compounded monthly. Payments will be made at the end of each month. Find the total value of the annuity in years.

Do not round any intermediate computations, and round your final answer to the nearest cent. If necessary, refer to the list of financial formulas.

Answer 1

The total value of the annuity in 19 years is approximately $10,602.97.

To find the total value of the annuity, we can use the future value formula for an annuity compounded monthly:

`\[ FV = P * ((1 + r)^(nt) - 1)/(r) \]`

Where:

- FV is the future value of the annuity.

- P is the monthly payment.

- r is the monthly interest rate (expressed as a decimal).

- n is the number of compounding periods per year.

- t is the number of years.

Given:

- P = 104 (monthly payment)

-
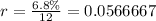`\( r = (6.8\%)/(12) = 0.0566667 \)` (monthly interest rate)

- n = 12 (monthly compounding)

- t = 19 years

Now, plug these values into the formula:

`\[ FV = 104 * ((1 + 0.0566667)^(12 * 19) - 1)/(0.0566667) \]`

Now calculate this expression using a calculator:

`\[ FV \approx 104 * ((1.0566667)^(228) - 1)/(0.0566667) \]`

`\[ FV \approx 104 * \frac {6.783078 - 1}{0.0566667} \]`

`\[ FV \approx 104 * (5.783078)/(0.0566667) \]`

`\[ FV \approx 104 * 102.0094 \]`

`\[ FV \approx 10,602.9744 \]`

So, the total value of the annuity in 19 years is approximately $10,602.97.

The probable question may be:

To save money for her son's college tuition, Christine invests dollar 104 every month in an annuity that pays 6.8% interest, compounded monthly. Payments will be made at the end of each month. Find the total value of the annuity in 19 years.

Do not round any intermediate computations, and round your final answer to the nearest cent. If necessary, refer to the list of financial formulas.