Answer:

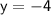
Explanation:
To solve the system of linear equations:

We can use the method of substitution or elimination. Let's use the substitution method.
Solve the first equation for one variable:
From the first equation, solve for
 :
:
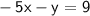
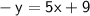
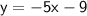
Substitute the expression into the second equation:
Substitute
 for
for
 in the second equation:
in the second equation:
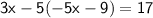
Solve for
 :
:
Solve the equation obtained in step 2 for
 :
:
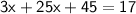
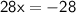
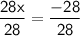

Substitute the value of
 back into one of the original equations to solve for
back into one of the original equations to solve for
 :
:
Use the first equation:
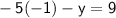
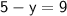
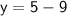
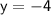
So, the solution to the system of equations is
 and
and
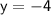 .
.