Only Triangle C has base and height proportional to the given triangle.
To determine whether the base and height of each triangle are proportional to the base and height of the given triangle, we can check if the ratios of corresponding sides are equal.
Given triangle with a 90-degree angle, base = 32 cm, and height = 10 cm.
![\[ \text{Given Triangle: } \, \, \, \, \, \, \, \frac{\text{base}}{\text{height}} = (32)/(10) = (16)/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/678ftrp35rigiwvpvvoarqekua0ddqlar6.png)
Now, let's check each option:
1. Triangle A:
![\[ (6.4)/(2) = (3.2)/(1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eab0o1346y9n90buitfta12ab57hhlyfs6.png)
This ratio is not equal to
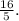
2. Triangle B:
![\[ (8)/(2.25) = (32)/(9) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vgbev0f6x89t93ygygqgy3y5fgcw9t3vxx.png)
This ratio is not equal to
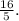
3. Triangle C:
![\[ (160)/(50) = (16)/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ryx8kxw344k3itnoq4cqvqdq8p08b59x4n.png)
This ratio is equal to
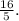
Therefore, only Triangle C has base and height proportional to the given triangle.