Explanation:
Given Information:
I'm assuming "A" and "B" are some constants that are coefficients as well as "m" and "n". Under this assumption we can take the derivative and then take the derivative once more to find the 2nd derivative which is denoted as:
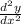
Chain Rule:
The chain rule can be denoted as:
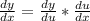
It can also be denoted in function notation as:

and in general it deals with composite functions and it it's going to help us take the derivative of the exponentials.
So take for example:
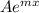 , we can rewrite this as a composite function where:
, we can rewrite this as a composite function where:
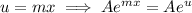
So from here we can just take the derivative of
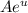 and then multiply it by the derivative of "u". We can also apply the same thing to
and then multiply it by the derivative of "u". We can also apply the same thing to
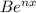
Calculating the First Derivative:
So let's first take the derivative of both sides, with respect to x
![(d)/(dx)[y]=(d)/(dx)[Ae^(mx) + Be^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8grrsshntqspmxsp8kyl.png)
From here we can take the derivative of
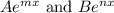 and then add them after taking the derivative individually.
and then add them after taking the derivative individually.
![(dy)/(dx)=(d)/(dx)[Ae^(mx)]+(d)/(dx)[Be^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/598dxaiz8a3e0x7xqe4z.png)
Assuming that "A" and "B" are constants, we can just take the derivative of:
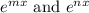 and then multiply by "A" and "B" after.
and then multiply by "A" and "B" after.
![(dy)/(dx)=A(d)/(dx)[e^(mx)]+B(d)/(dx)[e^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/dgzt4yymmd52fnrqtmbv.png)
now from here we apply the chain rule. I'll start with:
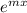 . First let's rewrite the equation so that we have a composite function:
. First let's rewrite the equation so that we have a composite function:
 now from here, we can apply the chain rule:
now from here, we can apply the chain rule:
![(d)/(dx)[e^(mx)]=(d)/(dx)[e^u]*(d)/(dx)[u]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/w3h2ukl79veffgitgefn.png)
You may know that the derivative of e to the x is just going to be e to the x, so the derivative of e^u is just e^u. Now substitute mx back in as u, and you get e^(mx). Now take the derivative of "u" which is just mx, and you get "m" since the derivative of any linear equation is just the slope (since this is constant):
![(d)/(dx)[e^(mx)]=e^(mx)*m](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/yvg2uiw16guenilh564w.png)
Now from here we can apply the same logic to e^(nx) to get:
![(d)/(dx)[e^(nx)]=e^(nx)*n](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9aifurbsbs15dxpaqquy.png)
So now we have the following expression:
![(dy)/(dx)=A[e^(mx)*m]+B[e^(nx)*n]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/d6fx1ohkic1uhj5r7qhv.png)
Calculating the Second Derivative:
![(d)/(dx)[(dy)/(dx)]=(d)/(dx)[A(e^(mx)*m)+B(e^(nx)*n)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o680yqtcrgl6do5xvo5d.png)
we can apply some of the rules we used before like taking each individual derivative then adding them after, and "factoring out" the A and B (because they're constants). This gives us the following expression:
![(d^2y)/(dx^2)=A(d)/(dx)[e^(mx)*m]+B(d)/(dx)[e^(nx)*n]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/nbcys1yqlzlxgnb28vtg.png)
From here we can also think of "factoring out" the m and n because they're constants, so we get the following:
![(d^2y)/(dx^2)=Am*(d)/(dx)[e^(mx)]+Bn*(d)/(dx)[e^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/mztoyxcdm9heiiqc5a4p.png)
From here we can apply the chain rule... except we already did this work (taking the derivative of e to the mx and e to the nx) so we can just put that here
![(d^2y)/(dx^2)=Am*[e^(mx)*m]+Bn*[e^(nx)*n]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zzdky1eyy8g3zmjjngox.png)
We can further simplify this to:
![(d^2y)/(dx^2)=Am^2*[e^(mx)]+Bn^2*[e^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5mcm9ohag12w44q44kiz.png)
Proving the Expression:
So we know that:
![(d^2y)/(dx^2)=Am^2*[e^(mx)]+Bn^2*[e^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5mcm9ohag12w44q44kiz.png)
and that:
![(dy)/(dx)=A[e^(mx)*m]+B[e^(nx)*n]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/d6fx1ohkic1uhj5r7qhv.png) or
or
![(dy)/(dx)=Am[e^(mx)]+Bn[e^(nx)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/g8nvizdqatd7wl5rxudj.png)
Plugging these into the expression:

we get the following:

First let's distribute the (m+n) to the first derivative to get:
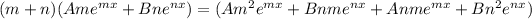
so plugging this in we get:

from here we can distribute the negative sign and cancel out values to get:
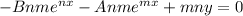
So we're almost done and it may look a bit weird in this situation since none of the variables look like they align to cancel them out... but notice how there is a "y" variable? We know what that is equal to! We started with that expression:
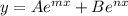
So let's plug this in to our expression:
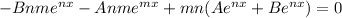
Let's distribute the "mn" using the distributive property:
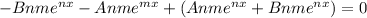
and from here we can finally cancel out all the values! and this simplifies to zero.
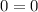
so we have proven that this expression is always equal to zero!