Question

Consider the following. f(x) = 4x3 − 6x2 − 24x + 4 (a) Find the intervals on which f is increasing or decreasing. (Enter your answers using interval notation.) increasing (−∞,−1)∪(2,∞) Correct: Your answer is correct. decreasing (−1,2) Correct: Your answer is correct. (b) Find the local maximum and minimum values of f. (If an answer does not exist, enter DNE.) local minimum value 4 Incorrect: Your answer is incorrect. local maximum value 4 Incorrect: Your answer is incorrect. (c) Find the intervals of concavity and the inflection points. (Enter your answers using interval notation.) concave up ( 1 2​,∞) Correct: Your answer is correct. concave down (−∞, 1 2​) Correct: Your answer is correct. inflection point (x, y) = 1 2​,−8.5 Incorrect: Your answer is incorrect.

Answer 1

(a) Increasing and Decreasing Intervals:

- Increasing: (-∞, -1) cup (2, ∞)

- Decreasing: (-1, 2)

(b) Local Maximum and Minimum:

- Local minimum values at (-1, -44) and (2, -52).

(c) Intervals of Concavity and Inflection Point:

- Concave up: (
`(1)/(2)`, ∞)

- Concave down: (-∞,
`(1)/(2)`)

- Inflection point at (
`(1)/(2)`, -8.5).

(a) Increasing and Decreasing Intervals:

To find where f(x) = 4x^3 - 6x^2 - 24x + 4 is increasing or decreasing, we analyze the sign of its derivative. The critical points occur where the derivative is zero or undefined. The intervals are:

- Increasing: (-∞, -1) cup (2, ∞)

- Decreasing: (-1, 2)

(b) Local Maximum and Minimum:

To find local maxima and minima, we examine the critical points. The derivative f'(x) = 12x^2 - 12x - 24 is set to zero: x = -1, 2 . Substituting these into f(x) , we find local minima at (-1, -44) and (2, -52) . No local maxima.

(c) Intervals of Concavity and Inflection Point:

The second derivative f''(x) = 24x - 12 determines concavity.

- Concave Up: (
`(1)/(2),` ∞)

- Concave Down: (-,
`(1)/(2)`)

- Inflection Point:
`\(((1)/(2), -8.5)\)`

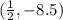
Therefore, f(x) is increasing on (-∞, -1) cup (2, ∞), decreasing on (-1, 2), has local minima at (-1, -44) and (2, -52), is concave up on (
`(1)/(2)`, ∞), concave down on (-∞,
`(1)/(2)`), and has an inflection point at
`\(((1)/(2), -8.5)\).`