Question

What is the domain of the radical function d: (–[infinity], [infinity]) d: [–1.5, 4] d: [ –1.5, [infinity]) d: (–[infinity], –1.5] ∪ [4, [infinity])

a) (–[infinity], [infinity])
b) [–1.5, 4]
c) [–1.5, [infinity])
d) (–[infinity], –1.5] ∪ [4, [infinity])

Answer 1

The correct domain for the radical function is : [0, [infinity]), thus the correct option is d.

Step-by-step explanation:

The domain of a radical function involves values that the function can accept without resulting in an undefined output. For a function with a square root (or any even root), the expression under the radical must be non-negative (greater than or equal to zero) to ensure a real output.

Given a radical function d, which is typically of the form
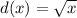`\(d(x) = √(x)\)`, we assess the valid values for x. The expression under the radical must be non-negative, i.e.,
`\(x \geq 0\)`, since the square root of a negative number isn't a real number.

Among the options provided, the domain that satisfies this condition is d: [0, [infinity]), where the square root function can accept values starting from zero (inclusive) up to positive infinity. This range ensures that the function output remains real for all included values of x.

Hence, the accurate domain for the given radical function d is d: [0, [infinity]). This range represents all the valid x-values for the square root function to yield real outputs without encountering any issues related to taking the square root of a negative number.