The answer is that the equation has two complex numbers as solutions.
The given quadratic equation is
 .
.
To determine the number of complex solutions, we can use the discriminant
 of the quadratic formula
of the quadratic formula
 , where
, where
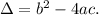
If
 is positive, the equation has two distinct real solutions.
is positive, the equation has two distinct real solutions.
If
 is zero, the equation has one real solution (a repeated or double root).
is zero, the equation has one real solution (a repeated or double root).
If
 is negative, the equation has two complex (conjugate) solutions.
is negative, the equation has two complex (conjugate) solutions.
In this case, the coefficients are a = 1 b = -10, and c = 41
Calculate
 :
:
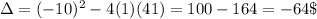
Since
 is negative
is negative
 , the quadratic equation
, the quadratic equation
 has two complex solutions.
has two complex solutions.
Therefore, the answer is that the equation has two complex numbers as solutions.
How many complex numbers this equation has. x² - 10x + 41 = 0
a) 1
b) 2
c) 3
d) 4