Question

Need help with this question someone explain it a picture is shown below

Answer 1

The total mass of the rod, with a linear density function
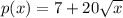`\( p(x) = 7 + 20√(x) \)` over 16 meters, is
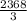`\( (2368)/(3) \)\\` kilograms.

To find the total mass of the rod, we need to integrate the linear density function p(x) over the length of the rod. The linear density function is given by
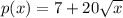`\( p(x) = 7 + 20√(x) \)` where x is measured in meters.

The total mass M of the rod is the integral of the linear density function over the length of the rod (from 0 to 16 meters in this case):

`\[ M = \int_(0)^(16) p(x) \, dx \]`

Substitute the given linear density function:

`\[ M = \int_(0)^(16) (7 + 20√(x)) \, dx \]`

Now, evaluate this definite integral:

`\[ M = \left[ 7x + (40)/(3)x^(3/2) \right]_(0)^(16) \]`

`\[ M = \left[ 7(16) + (40)/(3)(16)^(3/2) \right] - \left[ 7(0) + (40)/(3)(0)^(3/2) \right] \]`

`\[ M = 112 + (40)/(3) * 64 \]`

`\[ M = 112 + (1280)/(3) \]`

`\[ M = (2368)/(3) \]`

Therefore, the total mass of the rod is
`\( (2368)/(3) \)` kilograms.

The linear density of a rod of 16 m is given by
p(x) = 7+20\sqrt{x}
measure in kilogram per meter, where x is measured in meters from one end of the rod. Find the total mass of the rod?