Answer:
J (3; 9)
Explanation:
Imagine each distance like a triangle and use Pythagorean theorem.
To illustrate I drew triangle ΔLON in the picture
Finding the distance between LN.
LO =
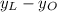 = 5 - 1 = 4
= 5 - 1 = 4
NO =
 = 5 - 4 = 1
= 5 - 4 = 1
According to Pythagorean theorem

 =
=
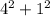 = 17
= 17
LN =
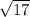 (LN > 0)
(LN > 0)
Since ΔMLN ≅ ΔKLJ, JL = LN (they are clearly equal triangles)
Mark J coordinates as (x; y)
Draw another triangle JOL, ∠JOL = 90°)
OJ is parallel with x axis and OL is parallel with y axis. O coordinates then are (4; y)
OL = y - 5
OJ = 4 - x
Note that ΔLON = ΔJOL, so OL is the same as LO and therefore
OL = LO = y - 5 = 4;
y = 9
OJ = NO = 4 - x = 1
x = 3
So the coordinates of J are (3; 9)
Similarly find the coordinates of K