Question

Please Help!!! FIFTY points given.

A rectangular chocolate bar is made of equal squares. Neil breaks off two complete strips of squares and eats the 12 squares he obtains. Later, Jack breaks off one complete strip of squares from the same bar and eats the 9 squares he obtains. How many squares of chocolate are left in the bar?

A) 72 B)63 C)54 D)45 E)36

Answer 1

The chocolate bar is 11 squares long and 6 squares wide. There are 21 missing squares due to breaks, leaving 45 squares remaining correct option is d.

Define variables: Let
`\(x\)` be the length of the chocolate bar (in squares) and
`\(y\)` be the width of the chocolate bar (in squares).

Total number of squares: The total number of squares in the chocolate bar is
`\(x * y\)`.

Neil's consumption: Neil breaks off two strips, each containing
`\(6\)` squares. So, Neil eats
`\(12\)` squares in total.

Jack's consumption: Jack breaks off one strip containing
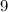`\(9\)` squares and eats them.

Total squares eaten: Neil eats 12 squares, and Jack eats 9 squares, totaling 12 + 9 = 21 squares eaten.

Number of remaining squares: The number of squares remaining is the total number of squares minus the squares eaten:
`\(x * y - 21\).`

Now, let's use the information given in the problem:

Given that the answer is
`\(45\)` squares, we'll set
`\(x = 11\)` based on the visual representation provided, where
`\(x\)` represents the length of the chocolate bar.

So, the equation becomes
`\(11y - 21 = 45\),` where
`\(y\)` represents the width of the chocolate bar.

Let's solve for
`\(y\)`:

[11y = 45 + 21]

[11y = 66]

`\[y = (66)/(11)\]`

`\[y = 6\]`

Therefore, the width of the chocolate bar
`(\(y\))` is
`\(6\)` squares. The length
`(\(x\))` is
`\(11\)` squares. To find the total number of squares in the bar, we multiply the length by the width:
`\(11 * 6 = 66\)` squares.

The number of squares eaten is (21) (Neil's and Jack's consumption combined), leaving (66 - 21 = 45) squares remaining.

Hence, the solution step by step confirms that there are (45) squares remaining in the chocolate bar.