Question

10) A roller coaster has a circular loop of radius 5.0 m. You go around at the minimum speed.

How fast will you be moving at the bottom?

What is your acceleration? (in m/s2, in g’s)

How does this feel? Where else have you felt this effect?

Draw a Force Diagram at the bottom.

This is dangerous. What should the radius be at the bottom, so that you only feel 2 g’s?
.
Explain why these loops have the shape that they do.

Answer 1

1) The speed of the roller coaster at the bottom is approximately 15.65 m/s

2) The acceleration of the roller coaster at the bottom is 6·g's

3) The high acceleration is 6 times the force of the weight of the passengers

The high acceleration can cause gravity induced loss of consciousness

4) Please find attached a force diagram of the forces at the bottom of the roller coaster created with Microsoft Visio

5) For the acceleration at the bottom to be 2·g's the radius of the rollercoaster at the bottom should be 25 meters

5) The radius at the bottom of roller coasters are increased to reduce the normal force felt by the passengers as they pass the bottom of a circular roller coaster

Step-by-step explanation:

1) The given parameters are;

The radius of the roller coaster, r = 5.0 m

The speed of the roller coaster = Minimum = 0 m/s

The shape of the roller coaster's path = Circular loop

Therefore, the maximum height of the roller coaster, h = The diameter of the of a circular path of the roller coaster, d = 2 × r = 2 × 5.0 m = 10.0 m

∴ h = 10.0 m

The minimum speed is f=given by the following equation;

`F_N = (m \cdot v^2)/(R) - m \cdot g = 0 \ (At \ the \ top \ of \ the \ roller \ coaster's \ path)`

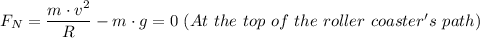
Therefore, we have;

`(m \cdot v^2)/(R) = m \cdot g`

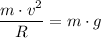
From which we have;

v = √(R × g)

Where;

R = The radius of the path of the roller coaster = 5.0 m

g = The acceleration due to gravity = 9.8 m/s² = constant

By plugging in the values of the variable, 'R', and the constant, 'g', we get;

v = √(5.0 m × 9.8 m/s²) = 7 m/s

The minimum speed of the roller coaster, v = 7 m/s

The speed of the roller coaster at the bottom is given by the conservation of energy formula as follows;

The energy at the top of the roller coaster = The energy at the bottom of the roller coaster

∴ The total mechanical energy of the roller coaster, M.E., is constant and at the top,
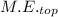`M.E._(top)`, is given as follows;

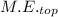`M.E._(top)` = 1/2·m·v₁² + m·g·h₁

At the bottom, the total mechanical energy is given as follows;

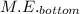`M.E._(bottom)` = 1/2·m·v₂² + m·g·h₂

Where;

v₁ = The velocity of the roller coaster at the top = 7 m/s

h₁ = The height of the roller coaster at the top = 10 m

v₂ = The speed of the roller coaster at the bottom

h₂ = The height of the roller coaster at the bottom = 0 m

g = The acceleration due to gravity = 9.8 m/s² = Constant

By plugging in the values, we get;

M.E. =
`M.E._(top)` =
`M.E._(bottom)`

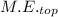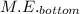
∴ 1/2·m·v₁² + m·g·h₁ = 1/2·m·v₂² + m·g·h₂

1/2 × (7 m/s)² + 9.8 m/s² × 10.0 m = 1/2 × v₂² + 9.8 m/s² × 0 m

122.5 m²/s² = 1/2 × v₂²

∴ v₂² = 2 × 122.5 m²/s² = 245 m²/s²

v₂ = √(245 m²/s²) = 7·√5 m/s ≈ 15.65 m/s

The speed of the roller coaster at the bottom, v₂ ≈ 15.65 m/s

2) The normal force on the car at the bottom of the roller coaster is given as follows;

`F_N = (m \cdot v_2^2)/(R) + m \cdot g = m * \left(( v_2^2)/(R) + g \right )`

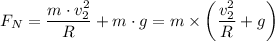
Force, F = Mass, m × Acceleration, a

∴ F = m×a

Therefore, the acceleration at the bottom, 'a' by comparison of the general equation for force, 'F', and the normal force,
`F_N`, is given as follows;

`a = \left(( v_2^2)/(R) + g \right )`

Plugging in the values for 'v₂²', 'R', ang 'g', gives;

`a = \left(( v_2^2)/(R) + g \right ) = \left(( 245)/(5) + 9.8 \right ) = \left(49+ 9.8 \right ) = (5 + 1) * 9.8 = 6 * 9.8 = 6 * g`

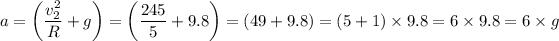
a = 6·g = 58.8 m/s²

3) The high acceleration will lead to a very high normal force (equal to 6 times each of their weight) experienced by the passengers with a force

The high acceleration is dangerous and can lead to gravity induced loss of consciousness since it is more than 3·g's

4) Please find attached the force diagram at the bottom of the roller coaster created with Microsoft Visio

5) For the acceleration at the bottom to be 2·g's, we have;

`a = \left(( v_2^2)/(R) + g \right )`

At a = 2·g, we have;

`2 \cdot g = \left(( v_2^2)/(R) + g \right )`

`\therefore 2 \cdot g - g = g = ( v_2^2)/(R)`

`R = ( v_2^2)/(g) = (245)/(9.8) = 25`

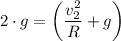
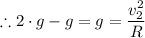
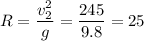
R = 25 m

The radius at the bottom of the roller coaster should be 25 meters so that only 2·g's is felt

5) The shape of the roller coaster has an increases the radius at the bottom so as to reduce the acceleration of the car