Final answer:
The final angle θf that the ball's velocity vector makes with the negative y-axis is θᵢ + vᵢδt.
Therefore, the correct answer is:
![\[ \boxed{\text{c) } \theta_i + v_i \delta t} \]](https://img.qammunity.org/2024/formulas/physics/high-school/clp7evaenvrpk208lymd13n4t3ku7kjkjh.png)
Step-by-step explanation:
To determine the final angle
 that the ball's velocity vector makes with the negative y-axis, we need to consider the change in angle
that the ball's velocity vector makes with the negative y-axis, we need to consider the change in angle
 during the time interval
during the time interval
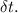
The change in angle
 is given by the angular displacement formula:
is given by the angular displacement formula:
![\[ \Delta \theta = \omega \cdot \delta t \]](https://img.qammunity.org/2024/formulas/physics/high-school/9xidrt9ohqhfuecqjgxaxf2ov2o2jnh3k2.png)
where
 is the angular velocity.
is the angular velocity.
For circular motion, the angular velocity
 is related to the linear velocity
is related to the linear velocity
 by the formula:
by the formula:
![\[ \omega = (v)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/whtw03mrpndzd4ifm0jylij2o5z0h4zh6b.png)
In this case, the radius
 is not given, but we can express
is not given, but we can express
 in terms of
in terms of
 and
and
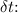
![\[ \omega = (\Delta \theta)/(\delta t) \]](https://img.qammunity.org/2024/formulas/physics/high-school/t8qdmavtgsin9h8lvgep0mpm1y4idel6tn.png)
Now, substitute the expression for
 in terms of
in terms of
 and
and
 into the angular displacement formula:
into the angular displacement formula:
![\[ \Delta \theta = (v)/(\delta t) \cdot \delta t \]](https://img.qammunity.org/2024/formulas/physics/high-school/fautiyzobd01lioic1tjz1ure6bdyaqm2c.png)
The
 cancels out, and we are left with:
cancels out, and we are left with:
![\[ \Delta \theta = v \]](https://img.qammunity.org/2024/formulas/physics/high-school/6dsosvyf1z6aeozzo1ix3oi6ibwsqe1she.png)
This means that the change in angle is equal to the initial velocity
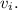
Now, the final angle
 is given by:
is given by:
![\[ \theta_f = \theta_i + \Delta \theta \]](https://img.qammunity.org/2024/formulas/physics/high-school/jvn68j6i1rlfkn9vfm8qab2skp6sdm5ref.png)
Substitute
 into the equation:
into the equation:
![\[ \theta_f = \theta_i + v_i \]](https://img.qammunity.org/2024/formulas/physics/high-school/jtptzhixlbn4hfxtbsl1euht00mhoqkcpx.png)
Therefore, the correct answer is:
![\[ \boxed{\text{c) } \theta_i + v_i \delta t} \]](https://img.qammunity.org/2024/formulas/physics/high-school/clp7evaenvrpk208lymd13n4t3ku7kjkjh.png)