Question

Compute the double integral of 1/(x²y²)da where R is the region bounded by the circles x² + y² = 4 and x² + y² = 9.

a. π/4
b. π/2
c. 2π
d. 4π

Answer 1

The double integral of
`\((1)/(x^2y^2)\)` over the region R bounded by the circles
`\(x^2 + y^2 = 4\)` and
`\(x^2 + y^2 = 9\)` is
`\((\pi)/(2)\)`.

The given double integral is expressed as:

`\[ \iint_R (1)/(x^2y^2) \,da \]`

To evaluate this integral over the region R, we can convert it to polar coordinates. The region R is defined by the circles
`\(x^2 + y^2 = 4\)` and
`\(x^2 + y^2 = 9\)`, which in polar coordinates become
`\(r = 2\) and \(r = 3\)`respectively.

The integral becomes:

`\[ \int_0^(2\pi) \int_2^3 (1)/(r^2 \cos^2(\theta) \sin^2(\theta)) \,r \,dr \,d\theta \]`

Solving this integral step by step:

1. Integrate with respect to r:
`\[ \int_2^3 (1)/(\cos^2(\theta) \sin^2(\theta)) \,dr \]`

2. Integrate with respect to
`\(\theta\)`:
`\[ \int_0^(2\pi) \,d\theta \]`

Evaluating these integrals will give the final result. The answer is
`\((\pi)/(2)\).`

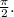
Therefore, the correct answer is option
`(b) \((\pi)/(2)\)`.