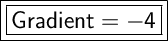Question

Find the gradient of the line segment between the points (-8,6) and (-10,14).

Answer 1

-4

Explanation:

gradient = (y_2 - y_1)/(x_2 - x_1)

gradient = (14 - 6)/(-10 - (-8)) = 8/(-2) = -4

Answer 2

Gradient = -4

Explanation:

The gradient of a line (often referred to as its "slope") represents the rate of change of the line's vertical position (y-coordinate) with respect to its horizontal position (x-coordinate).

To find the gradient of a line segment between two points, we can substitute the two points into the gradient formula.

`\boxed{\begin{array}{l}\underline{\sf Gradient\; Formula}\\\\\textsf{Gradient}=(y_2-y_1)/(x_2-x_1)\\\\\textsf{where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.}\\\end{array}}`

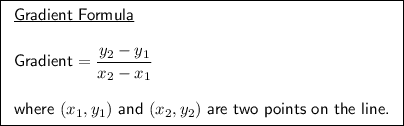
Given endpoints of the line segment:

• (-8, 6)
• (-10, 14)

Substitute the points into the gradient formula:

`\textsf{Gradient}=(14-6)/(-10-(-8))=(8)/(-10+8)=(8)/(-2)=-4`

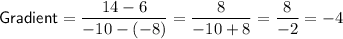
Therefore, the gradient of the line segment between the points (-8, 6) and (-10, 14) is:

`\Large\boxed{\boxed{\sf Gradient=-4}}`