Question

Using Rydberg’s equation, determine the wavelength of the lines where ni = 3 and nf = 2, with Rh = 1.097e7 m⁻¹.

a) 3.2e⁻⁷ m
b) 4.5e⁻⁷ m
c) 5.8e⁻⁷ m
d) 7.1e⁻⁷ m

Answer 1

The wavelength of the lines where ni = 3 and nf = 2, with Rh = 1.097e7 m⁻¹, using Rydberg’s equation is 4.5e⁻⁷ m (4.5×
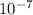`10^(-7)` m). (option b)

Step-by-step explanation:

Rydberg’s equation for the calculation of the wavelength (λ) of a spectral line is given by:

1/λ = R_H(1/n_f²-1/n_i²)

Where:

λ is the wavelength,

R_H is the Rydberg constant (1.097×
`10^(-7)`
`m^(-1)`),

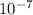
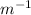n_f is the final principal quantum number,

n_i is the initial principal quantum number.

In this case, n_i = 3 and n_f = 2. Substituting these values into the equation:

1/λ = (1.097×
`10^(-7)`
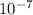
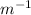`m^(-1)`) (1/2²-1/3²)

Solving for λ:

1/λ = 1/1/2²-1/3²×1.097×
`10^(-7)`

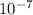
λ ≈ 4.5×
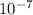`10^(-7)` m

The wavelength of the spectral line, where the electron transitions from n_i = 3 to n_f = 2 based on Rydberg’s equation, is approximately (1.097×
`10^(-7)`
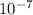
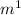`m^(1)`). This corresponds to the visual range of the electromagnetic spectrum, making it consistent with the characteristics of certain atomic transitions observed in visible light. The correct option among the choices provided is b) 4.5e⁻⁷ m