Answer:
The length is 7 m
The width is 10 m
Explanation:
length = x
width = 2x - 4
length * width = area
It is given that the area is 70

From there
x * (2x - 4) = 70
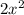 - 4x = 70
- 4x = 70
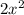 - 4x - 70 = 0
- 4x - 70 = 0
 - 2x - 35 = 0
- 2x - 35 = 0
Now we have a quadratic equation, which is a
 + bx + c = 0, where a
+ bx + c = 0, where a
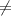 0
0
In this equation a = 1, b = -2 and c = -35
Discriminant (D) formula is b² - 4ac
D =
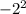 - 4 * 1 * (-35) = 144 > 0
- 4 * 1 * (-35) = 144 > 0
This discriminant is more than 0, so there are two possible x
Their formulas are
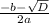 and
and
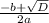
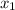 =
=
 = -5 < 0 (the length of the rectangle has to be more than 0, so we don't use this x)
= -5 < 0 (the length of the rectangle has to be more than 0, so we don't use this x)
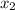 =
=
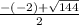 = 7 > 0 (this one is right)
= 7 > 0 (this one is right)
Calculating the dimensions
length = x = 7 (m)
width = 2x - 4 = 2 * 7 - 4 = 10 (m)