Question

An undiscovered planet, many lightyears from Earth, has one moon

in a periodic orbit. This moon takes 15601560 ×
103 seconds (about 1818 days) on average
to complete one nearly circular revolution around the unnamed
planet. If the distance from the center of the moon to the surface
of the planet is 245.0245.0 × 106 m and
the planet has a radius of 3.103.10 ×
106 m, calculate the moon's
radial acceleration cac.
ac= ?

Answer 1

The radial acceleration
`(\(a_c\))` of the moon in its periodic orbit around the undiscovered planet is approximately
`\(1.08 \, m/s^2\).`

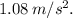
Step-by-step explanation:

To calculate the radial acceleration
`(\(a_c\)),` we can use the formula for centripetal acceleration:

`\[ a_c = (v^2)/(r) \]`

where \(v\) is the tangential velocity and
`\(r\)` is the radial distance from the center. First, we need to find the tangential velocity, which can be determined using the formula:

`\[ v = (2 \pi r)/(T) \]`

where T is the period of revolution. Substituting the given values, we find
`\(v \approx 5.46 * 10^3 \, m/s\).` Now, we can substitute this into the centripetal acceleration formula:

`\[ a_c = ((5.46 * 10^3)^2)/(2.45 * 10^6) \]`

Solving this expression yields
`\(a_c \approx 1.08 \, m/s^2\).`

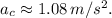
In summary, the moon's radial acceleration in its periodic orbit around the planet is approximately
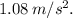`\(1.08 \, m/s^2\).` This calculation involves the tangential velocity and radial distance, providing insights into the gravitational forces governing the moon's motion.