Question

Triangle RST was dilated with the origin as the center of dilation to create triangle R'S'T'. The triangle was dilated using a scale factor of 34.

The lengths of the sides of triangle RST are given.

Enter the lengths of the sides of triangle R'S'T' below.
(Decimal values may be used.)

Answer 1

RS =6

ST =7.5

RT =9

When a triangle is dilated with the origin as the center of dilation, the coordinates of each point in the original triangle are scaled by the same factor to obtain the coordinates of the corresponding points in the new triangle. The scale factor (k) in this case is given as 3/4. Let's denote the coordinates of the vertices of the original triangle RST as (x, y), and the coordinates of the vertices of the new triangle R'S'T' as (x', y'). The relationship between the coordinates of corresponding points in the original and new triangles is given by:

`x^(') = kx\\y^(') = ky`

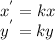
Now, let's apply this to each vertex of the triangle RST

`x^(')_(R) = (3)/(4) x\\y^(')_(R)= (3)/(4) y`

`x^(')_(S) = (3)/(4) x\\y^(')_(S)= (3)/(4) y`

`x^(')_(T) = (3)/(4) x\\y^(')_(T)= (3)/(4) y`

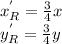
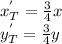
The original side lengths are RS = 8, ST = 10, and RT = 12. The corresponding side lengths in the new triangle R'S'T' are obtained by multiplying the original side lengths by the scale factor

RS' =
`(3)/(4) . 8` = 6

ST' =
`(3)/(4) . 10` = 7.5

RT' =
`(3)/(4) . 12` = 9

The lengths of the sides in the new triangle R'S'T' are:

RS =6

ST =7.5

RT =9

Question

Attached as image.