Question

A rectangular swimming pool is twice as long as it is wide. A small concrete walkway surrounds the pool. The walkway is a 2 feet wide and has an area of 448 square feet including the pool.Find the dimensions of the pool

Answer 1

The width and the length of the pool are 12 ft and 24 ft respectively.

Explanation:

The length (L) of the rectangular swimming pool is twice its wide (W):

`L_(1) = 2W_(1)`

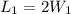
Also, the area of the walkway of 2 feet wide is 448:

`W_(2) = 2 ft`

`A_(T) = W_(2)*L_(2) = 448 ft^(2)`

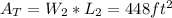
Where 1 is for the swimming pool (lower rectangle) and 2 is for the walkway more the pool (bigger rectangle).

The total area is related to the pool area and the walkway area as follows:

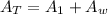`A_(T) = A_(1) + A_(w)` (1)

The area of the pool is given by:

`A_(1) = L_(1)*W_(1)`

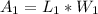
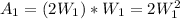`A_(1) = (2W_(1))*W_(1) = 2W_(1)^(2)` (2)

And the area of the walkway is:

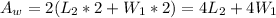`A_(w) = 2(L_(2)*2 + W_(1)*2) = 4L_(2) + 4W_(1)` (3)

Where the length of the bigger rectangle is related to the lower rectangle as follows:

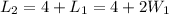`L_(2) = 4 + L_(1) = 4 + 2W_(1)` (4)

By entering equations (4), (3), and (2) into equation (1) we have:

`A_(T) = A_(1) + A_(w)`

`A_(T) = 2W_(1)^(2) + 4L_(2) + 4W_(1)`

`448 = 2W_(1)^(2) + 4(4 + 2W_(1)) + 4W_(1)`

`224 = W_(1)^(2) + 8 + 4W_(1) + 2W_(1)`

`224 = W_(1)^(2) + 8 + 6W_(1)`

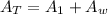
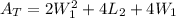
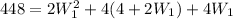
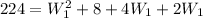
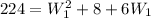
By solving the above quadratic equation we have:

W₁ = 12 ft

Hence, the width of the pool is 12 feet, and the length is:

`L_(1) = 2W_(1) = 2*12 ft = 24 ft`

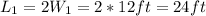
Therefore, the width and the length of the pool are 12 ft and 24 ft respectively.

I hope it helps you!