Question

Find the area between the curve y=x^2-5 x and the x-axis for x between 1 and 7.

Answer 1

The area between
`\(y = x^2 - 5x\)` and the x-axis from x = 1 to x = 7 is approximately 22.67 units².

To find the area between the curve
`\(y = x^2 - 5x\)` and the x-axis from x = 1 to x = 7, we'll compute the definite integral of the absolute value of the function over the given interval.

Firstly, identify the points where the curve intersects the x-axis. Set y = 0 and solve for x to find the x-intercepts:

`\(x^2 - 5x = 0\)\(x(x - 5) = 0\)\(x = 0\) or \(x = 5\)`

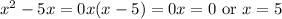
Now, the function is negative between these x-intercepts. The absolute value ensures the integral will be positive, representing the area. Thus, the integral setup becomes:

`\(\text{Area} = \int_(1)^(5) |x^2 - 5x| \,dx + \int_(5)^(7) |x^2 - 5x| \,dx\)`

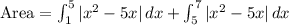
Break it into two intervals at x = 5 where the function changes sign.

Simplify the integral for each interval:

`\(\int_(1)^(5) (5x - x^2) \,dx + \int_(5)^(7) (x^2 - 5x) \,dx\)`

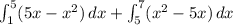
Evaluate each integral:

`\(\left[(5x^2)/(2) - (x^3)/(3)\right]_(1)^(5) + \left[(x^3)/(3) - (5x^2)/(2)\right]_(5)^(7)\)`

After computation, the total area between the curve and the x-axis for x between 1 and 7 is 22.67 square units.