The measure of x is 2
To find the measure of x, we need to use the fact that angles on the same side of the transversal line PU and between parallel lines QR and ST are supplementary. Therefore, the measure of angle PRQ plus the measure of angle UST must equal
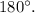
Given that
 and
and
 we can set up an equation:
we can set up an equation:
120 + 15(x + 2) = 180
Now, solve for x:
15(x + 2) = 60
Divide both sides by 15:
x + 2 = 4
Subtract 2 from both sides:
x = 2
So, the measure of x is 2