Final answer:
Elementary row operations on matrices are used to transform a given matrix into an equivalent matrix in row-echelon form or reduced row-echelon form.
Explanation:
Elementary row operations on matrices are operations that can be performed on the rows of a matrix to obtain an equivalent matrix. These operations are used to transform a given matrix into an equivalent matrix in row-echelon form or reduced row-echelon form.
Row-echelon form is a matrix with the property that all zero rows are at the bottom, and the leading coefficient of each non-zero row is strictly to the right of the leading coefficient of the row above it. A matrix is said to be in reduced row-echelon form when all the leading coefficients are 1.
The elementary row operations are: row interchanges, row addition and row multiplication. Row interchanges involve switching two rows of the matrix. Row addition involves adding a multiple of one row of the matrix to another. Row multiplication involves multiplying a row of the matrix by a non-zero scalar.
These operations are applied to a given matrix to transform it into an equivalent matrix in row-echelon form or reduced row-echelon form. This form of the matrix can be used to solve linear systems of equations, to calculate the determinant of the matrix, and to find the inverse of the matrix.
For example, consider the following matrix:
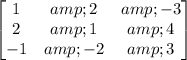
By applying elementary row operations, we can transform this matrix to a matrix in row-echelon form:
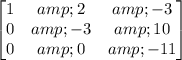
This form of the matrix is useful for solving linear systems of equations, calculating the determinant, and finding the inverse of the matrix.
In conclusion, elementary row operations are used to transform a given matrix into an equivalent matrix in row-echelon form or reduced row-echelon form. This form of the matrix is useful for solving linear systems of equations, calculating the determinant, and finding the inverse of the matrix.