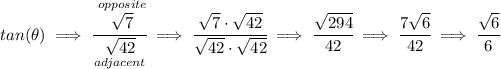Question

Evaluate without a calculator: tan (sin-1 ((√ 7)/7)​

Answer 1

let's say for a second that that angle is θ, so we can say that

`sin^(-1)\left(\cfrac{√(7)}{7} \right)=\theta \qquad therefore\qquad tan\left[ sin^(-1)\left(\cfrac{√(7)}{7} \right) \right]\implies tan(\theta ) \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{this really means}}{sin^(-1)\left(\cfrac{√(7)}{7} \right)=\theta}\implies \cfrac{\stackrel{opposite}{√(7)}}{\underset{hypotenuse}{7}}=sin(\theta )`

let us notice something, the opposite side is positive, that means either the I or II Quadrant, however the sin⁻¹ function has a range constrained to π/2 to -π/2, which excludes the II Quadrant, so that means that θ must be on the I Quadrant, where the adjacent side or cosine or "x" is positive too.

now, let's use the pythagorean theorem to get the adjacent side for θ

`\textit{using the pythagorean theorem} \\\\ c^2=a^2+b^2\implies √(c^2-b^2)=a \qquad \begin{cases} c=\stackrel{hypotenuse}{7}\\ a=adjacent\\ b=\stackrel{opposite}{√(7)}\\ \end{cases} \\\\\\ \pm\sqrt{7^2-(√(7))^2}=a\implies \pm√(42)=a\implies \stackrel{I~Quadrant}{+√(42)=a} \\\\[-0.35em] \rule{34em}{0.25pt}`

`tan(\theta )\implies \cfrac{\stackrel{opposite}{√(7)}}{\underset{adjacent}{√(42)}}\implies \cfrac{√(7)\cdot √(42)}{√(42)\cdot √(42)}\implies \cfrac{√(294)}{42}\implies \cfrac{7√(6)}{42}\implies \cfrac{√(6)}{6}`