The solution to
 is x < -20 or x > 36. The graph consists of two unconnected intervals on the number line.
is x < -20 or x > 36. The graph consists of two unconnected intervals on the number line.
Part A: Solve the Inequality
![\[ | (1)/(4)x - 2| - 3 > 4 \]](https://img.qammunity.org/2024/formulas/mathematics/college/11mn2tu63cqp7wht9sdlkv9efafrvs6soh.png)
1. Isolate the Absolute Value Term:
![\[ | (1)/(4)x - 2| > 7 \]](https://img.qammunity.org/2024/formulas/mathematics/college/81hty6ep15kvzpo4yc935tys4b3n8txz7p.png)
2. Set up Two Cases:
![\[ (1)/(4)x - 2 > 7 \quad \text{or} \quad -((1)/(4)x - 2) > 7 \]](https://img.qammunity.org/2024/formulas/mathematics/college/7fm02e37grdtzbd5pd8okadsy0gp4d97cn.png)
3. Solve Each Case Separately:
- Case 1:
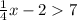
![\[ (1)/(4)x > 9 \]](https://img.qammunity.org/2024/formulas/mathematics/college/9eeegd398giou91xs9zltbl2v42blsmvxx.png)
x > 36
- Case 2:
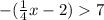
![\[ -(1)/(4)x + 2 > 7 \]](https://img.qammunity.org/2024/formulas/mathematics/college/rhgrfsl47jyuqgwlbcckuq9auuyns2k0xn.png)
![\[ -(1)/(4)x > 5 \]](https://img.qammunity.org/2024/formulas/mathematics/college/xrx5ojyulpwuqgng078obwggj43opk77sc.png)
x < -20
4. Combine the Solutions:
![\[ x < -20 \text{ or } x > 36 \]](https://img.qammunity.org/2024/formulas/mathematics/college/d4nh7logdk4ekwob3nnbsq41m0z5uy3ogf.png)
Part B: Describe the Graph of the Solution
The solution represents all real numbers except those between -20 and 36, forming two unconnected intervals on the number line.