Solve for x (x)/(2) -(x)/(5)=2 Give your answer in its simplest form.

Question

Solve for x


`(x)/(2)` -
`(x)/(5)`=2

Give your answer in its simplest form.

Answer 1

Explanation:

`\tt{ (x)/(2) - (x)/(5) = 2}`

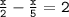
Take the L.C.M of 2 & 5. It's ' 10 '. Firstly find out the factors of 2 [ i.e 1 × 2 ] and then secondly find out the factors of 5 [ i.e 1 × 5 ]. Now , Note that while finding L.C.M of any numbers, Common numbers & Remaining numbers must be multiplied. In our case , common number = 1 & Remaining numbers are 2 & 5. Multiply them : [ 1 × 2 × 5 = 10 ].

⟶
`\tt{ (x * 5 - x * 2)/(10) = 2}`

⟶
`\tt{ (5x - 2x)/(10) = 2}`

Subtract 2x from 5x :

⟶
`\tt{ (3x)/(10) = 2}`

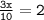
Apply cross product property :

⟶
`\tt{3x * 1 = 2 * 10}`

⟶
`\tt{3x = 20}`

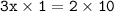
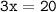
Here, We have to think about how to remove the coefficient 3. For that , Divide both sides of the equation by 3.

⟶
`\tt{ (3x)/(3) = (20)/(3)}`

⟶
`\tt{x =6.67}`

`\pink {\boxed{ \boxed{ \tt{⇾ Our \: final \: answer : \boxed{ \underline{ \tt{x = (20)/(3) \: or \: 6.67 }}}}}}}`

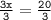
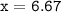
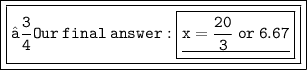
Hope I helped ! ♡

Have a wonderful day / night ! ツ

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁