Question

Suppose point A is located at (1, 3) on a coordinate plane. If AB is 10 and the x-coordinate of point B is 9, explain how to use the Distance Formula to find the y-coordinate of point B.

Answer 1

To find the y-coordinate of point B, you can use the Distance Formula. By substituting the given values into the formula and simplifying, you find that the y-coordinate of point B can be either 3 + √19 or 3 - √19.

Step-by-step explanation:

To find the y-coordinate of point B, we can use the Distance Formula. The formula is:

`d = \sqrt{((x2 - x1)^2 + (y2 - y1)^2)`

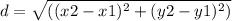
Given that point A is located at (1, 3) and the x-coordinate of point B is 9, we can substitute these values into the formula:

`d = \sqrt{((9 - 1)^2 + (y2 - 3)^2)`

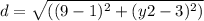
Since AB is 10, we can replace d with 10 and simplify:

`10 = \sqrt{((9 - 1)^2 + (y2 - 3)^2)`

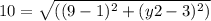
Squaring both sides of the equation:

`100 = (9 - 1)^2 + (y2 - 3)^2`

`81 + (y2 - 3)^2 = 100`

`(y2 - 3)^2 = 100 - 81`

`(y2 - 3)^2 = 19`

`y2 - 3 = +/-\sqrt{19`

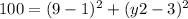
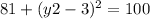
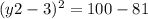
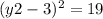
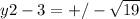
So, the y-coordinate of point B can be either 3 + √19 or 3 - √19.

Answer 2

y =9

Step-by-step explanation:

you know the distance is 10 and some of the x,y points. so start filling what you know into the distance formula

10= √((9-1)^2 + (y-3)^2 )

square both sides to get ride of the square root

100 = 64 + (y-3)^2

36 = (y-3)^2

6 = y-3

y = 9

double check by using 9 for Y and you'll see it works.