Question

Write an equation in standard form of the line that passes through (3,1) and has a y-intercept of -2. (Please write it in this form) x + y = __ <-- the number thats supposed to go there.

Answer 1

x - y = 2

Explanation:

To write an equation in standard form of the line that passes through (3, 1) and has a y-intercept of -2, we can use the slope-intercept form of a linear equation:

`\boxed{\begin{array}{l}\underline{\textsf{Slope-intercept form of a linear equation}}\\\\\large\text{$y=mx+b$}\\\\\textsf{where:}\\\phantom{ww}\bullet\;\;\textsf{$m$ is the slope.}\\\phantom{ww}\bullet\;\;\textsf{$b$ is the $y$-intercept.}\\\end{array}}`

In this case:

• x = 3
• y = 1
• b = -2

Substitute these values into the formula and solve for the slope (m):

`\begin{aligned}1&=m(3)-2\\1&=3m-2\\1+2&=3m-2+2\\3&=3m\\m&=1\end{aligned}`

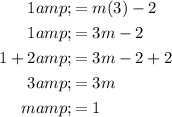
Substitute the slope (m = 1) and the y-intercept (b = -2) into the slope-intercept form:

`y=x-2`

The standard form of a linear equation is Ax + By = C, where A, B and C are constants, and the coefficient of x is always non-negative.

`\boxed{\begin{array}{l}\underline{\textsf{Standard form of a linear equation}}\\\\Ax+By=C\\\\\textsf{where:}\\ \phantom{ww}\bullet\;\textsf{$A, B$ and $C$ are constants.}\\\phantom{ww}\bullet\;\textsf{$A$ must be positive.}\end{array}}`

Therefore:

`\begin{aligned}y&=x-2\\y+2&=x-2+2\\y+2&=x\\y+2-y&=x-y\\2&=x-y\\x-y&=2\end{aligned}`

So, the equation of the line that passes through (3, 1) and has a y-intercept of -2 is:

`\Large\boxed{\boxed{x-y=2}}`

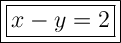
Please note that this equation cannot be rearranged in the form x + y = ?