Find the area of the surface of a circular pound that has a diameter of 12 metre

Question

asked Oct 25, 2022 196k views

2 Answers

Slaven Rezic · Answer 1 · 2022-10-26T05:46:32+0000

Using the formulas

Solving forA

__________________________________

this is your answer

Terek · Answer 2 · 2022-10-30T15:34:43+0000

$\Large \underline{\tt Given} :$

$\\$

$\Large \underline{\tt To \: Find} :$

$\\$

$\Large \underline{\tt Solution} :$

As, pound in circular in shape, so to find it's area we have a formula :

$\underline{\boxed{\bf{Area_((circle)) = \pi r^2}}}$

$\\$

Now, we have diameter of circular pound, D = 12 m.

So, Radius of circular pound, r =
$\tt (D)/(2)$

⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀=
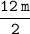
$\tt \cancel{(12 \: m)/(2)}$

⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀⠀ ⠀=
$\tt 6 \: m$

$\\$

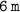
Now, by substituting value of π = 22/7 and r = 6 m, we have area of circle :

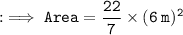
$\tt : \implies Area = (22)/(7) * (6 \: m)^(2)$

$\tt : \implies Area = (22)/(7) * 36 \: m^(2)$

$\tt : \implies Area = (792)/(7) \: m^(2)$

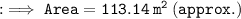
$\tt : \implies Area = 113.14 \: m^(2) \: (approx.)$

Hence, Area of the surface of circular pound is approximately 113.14 m².