Question

Which of the following properties can be used to show that the expression 4^{\frac{5}{3}} is equivalent to \sqrt[3]{4^{5}}?

Answer 1

The correct property to show that
`\(4^(5/3)\)` is equivalent to
`\(\sqrt[3]{4^5}\)` is: B.
`\((4^(5/3))^3 = 4^((5/3) * 3) = 4^5\)`

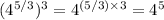
Let's show the work for option B:

`\((4^(5/3))^3 = 4^((5/3) * 3) = 4^5\)`

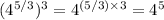
First, we use the property of exponents that states when you raise a power to another power, you multiply the exponents.

`\((4^(5/3))^3 = 4^((5/3) * 3)\)`

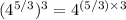
Now, multiply the exponents inside the parentheses:

`\(4^((5/3) * 3) = 4^5\)`

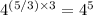
This shows that
`\(4^(5/3)\)` raised to the power of 3 is indeed equal to
`\(4^5\)`, confirming the equivalence with the cube root of
`\(4^5\)`.

This property demonstrates the equivalence by showing that raising
`\(4^(5/3)\)` to the power of 3 results in
`\(4^5\)`, confirming the equality between the given expression and the cube root of
`\(4^5\)`.

Option B is correct.