Question

A factory produce bicycles at a rate of 110+0.5t^2-0.9t bicycles per week (t in weeks)

how many bicycles were produced from 8 to 2

Answer 1

221

Explanation:

Day 8 is the first day of the second week.

Day 21 is the last day of week 3.

We need to know the n umber of bicycles made from t = 1 to t = 3

The function is b(t) = 110 + 0.5t^2 - 0.9t, where t is in weeks.

We need to integrate the function with the limits of 1 to 3.

`\int_(1)^(3) (110 + 0.5t^2 - 0.9t) dt`

`\int_(1)^(3) (110 + (t^2)/(2) - (9t)/(10)) dt`

`= 110t + (t^3)/(6) - (9t^2)/(20) \Biggr|_(1)^(3)`

`= 330.45 - 109.72`

`= 220.7333`

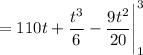
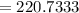
Answer: 221