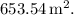The total surface area of the cylinder is approximately
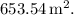
The curved surface area (CSA) of a cylinder is given by the formula
 , where r is the radius and h is the height (or length in this case).
, where r is the radius and h is the height (or length in this case).
In this problem, you are given

![\[ 546\pi = 2\pi r * 21 \]](https://img.qammunity.org/2024/formulas/mathematics/college/88tiluwh95cgay5bczg323mr5l958v5bq7.png)
Now, solve for r:
![\[ r = (546\pi)/(2\pi * 21) \]](https://img.qammunity.org/2024/formulas/mathematics/college/nhef10phi4vjkie1c0i8e38ayotdb3l724.png)
![\[ r = (546)/(42) \]](https://img.qammunity.org/2024/formulas/mathematics/college/o0ea3fb8sedeswph32gj4b4er9emwpa6ki.png)
![\[ r = 13 \, \text{m} \]](https://img.qammunity.org/2024/formulas/mathematics/college/oap8610yi1llfcc4fe28d1g3xecr9folxj.png)
Now, to find the total surface area (TSA) of the cylinder, we use the formula
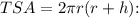
![\[ TSA = 2\pi * 13 * (13 + 21) \]](https://img.qammunity.org/2024/formulas/mathematics/college/srfnlej23hwcyox2ckmjyo2zn20bsj3zq8.png)
![\[ TSA = 2\pi * 13 * 34 \]](https://img.qammunity.org/2024/formulas/mathematics/college/bfkyfcjdpybue6rxq4snaqrc8526nj1c59.png)
![\[ TSA \approx 653.54 \, \text{m}^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/vualiybl7xviqwvgspl7vrc4guhodds0mu.png)
Therefore, the total surface area of the cylinder is approximately