Question

How many roots does this has?
x^2+(2√5x)+2x=-10​
find Discriminant

Answer 1

Given:

The equation is

`x^2+(2√(5))+2x=-10`

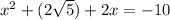
To find:

The number of roots and discriminant of the given equation.

Solution:

We have,

`x^2+(2√(5))x+2x=-10`

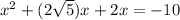
The highest degree of given equation is 2. So, the number of roots is also 2.

It can be written as

`x^2+(2√(5)+2)x+10=0`

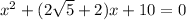
Here,
`a=1, b=(2√(5)+2), c=10`.

Discriminant of the given equation is

`D=b^2-4ac`

`D=(2√(5)+2)^2-4(1)(10)`

`D=20+8√(5)+4-40`

`D=8√(5)-16`

`D\approx 1.89>0`

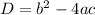
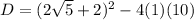
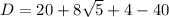
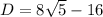
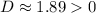
Since discriminant is
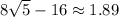`8√(5)-16\approx 1.89`, which is greater than 0, therefore, the given equation has two distinct real roots.