Question

Bob kicked a soccer ball a total horizontal distance of 30 feet. The football reached a maximum height of 10 feet. The ball moved in a path that was parabolic. Determine the equation of the parabola in graphing form.

Answer 1

The parabolic equation for Bob's soccer ball motion is
`\(y = -2(x - 15)^2 + 10\)` in graphing form.

To determine the equation of the parabola in graphing form, we can use the standard form of the equation for a parabola, which is
`\(y = a(x - h)^2 + k\)`, where (h, k) is the vertex of the parabola.

In this case, the soccer ball's path is parabolic, so we can consider the motion in the horizontal (x) and vertical (y) directions separately. The horizontal motion is uniform, so the equation for the horizontal distance traveled (x) can be given by x = vt, where v is the horizontal velocity of the ball and \(t\) is the time.

Since the vertical motion is affected by gravity, we can use the equation
`\(y = -16t^2 + vt + h\)`, where h is the initial height. At the maximum height, the vertical velocity
`(\(v_y\))` is zero, so we can find the time it takes to reach the maximum height
`(\(t_{\text{max}}\))` using
`\(v_y = -32t_{\text{max}} + v\).`

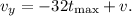
Now, we can use the values given to find the vertex
`(\((h, k)\))` and substitute them into the standard form of the parabola equation
`\(y = a(x - h)^2 + k\).`Finally, we get the equation of the parabola in graphing form.