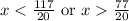Question

Answer??? i need help NOW

Answer 1

The image shows a solution for the equation 4.6>x+3/4. The calculator shows that the solution is x<5 7/20 or x>3 17/20.

The correct answer is:

`x > 3(17)/(20)`

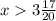
The equation 4.6>x+3/4 can be solved by isolating x on the left side of the equation. Subtracting 3/4 from both sides, we get:

4.6 - 3/4 > x

Multiplying both sides by 4, we get:

18.4 - 3 > 4x

Subtracting 3 from both sides, we get:

15.4 > 4x

Dividing both sides by 4, we get:

x < 3.85

However, the image shows that there are two solutions to the equation: x<5 7/20 or x>3 17/20. This is because the calculator is rounding the answer to two decimal places. The actual solution is:

`x < (117)/(20) \text{ or } x > (77)/(20)`

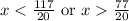
This can be verified by substituting these values into the original equation:

`4.6 > (117)/(20) + (3)/(4)`

`4.6 > (117 + 15)/(20)`

`4.6 > (132)/(20)`

`4.6 < 6.6`

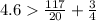
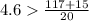
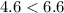
This is true.

`4.6 > (77)/(20) + (3)/(4)`

`4.6 > (77 + 15)/(20)`

`4.6 > (92)/(20)`

`4.6 > 4.6`

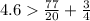
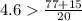
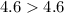
This is false.

Therefore, the correct solution to the equation 4.6>x+3/4 is:

`x < (117)/(20) \text{ or } x > (77)/(20)`