Question

THE RIGHT ANSWER WILL RECEIVE A BRAINLESS AND POINTS AND THANKS!!! THE RIGHT ANSWER WILL RECEIVE A BRAINLESS AND POINTS AND THANKS!!! What is the fundamental frequency of a mandolin string that is 42.0 cm long when the speed of waves of the string is 329 m/s? with working outs

Answer 1

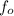`f_(o)` = 391.67 Hz

Step-by-step explanation:

The sound of lowest frequency which is produced by a vibrating sting is called its fundamental frequency (
`f_(o)`).

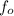The For a vibrating string, the fundamental frequency (
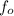`f_(o)`) can be determined by:

`f_(o)` =
`(v)/(2L)`

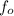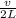
Where v is the speed of waves of the string, and L is the length of the string.

L = 42.0 cm = 0.42 m

v = 329 m/s

`f_(o)` =
`(329)/(2*0.42)`

=
`(329)/(0.84)`

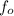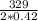
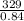
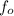`f_(o)` = 391.6667 Hz

The fundamental frequency of the string is 391.67 Hz.