1 Answer

Scottmf · Answer 1 · 2022-12-14T10:08:50+0000

Given:

The equation of line is

4x+3y=12

To find:

The points on y-axis which are at a distance of 4 units from the given line.

Solution:

The point lie on the y-axis. So, their x-coordinate must be zero.

Let the points are in the form of (0,k).

The distance between a point
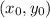(x_0,y_0) and a line
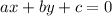ax+by+c=0 is

d=(|ax_0+by_0+c|)/(√(a^2+b^2))

The given equation can be written as

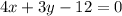
4x+3y-12=0

The distance between (0,k) and
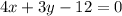4x+3y-12=0 is 4 units.

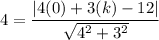
4=(|4(0)+3(k)-12|)/(√(4^2+3^2))

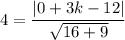
4=(|0+3k-12|)/(√(16+9))

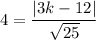
4=(|3k-12|)/(√(25))

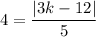
4=(|3k-12|)/(5)

Multiply both sides by 5.

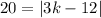
20=|3k-12|

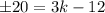
$\pm 20=3k-12$

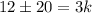
$12\pm 20=3k$

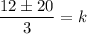
$(12\pm 20)/(3)=k$

Now,

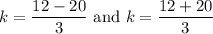
$k=(12-20)/(3)\text{ and }k=(12+20)/(3)$

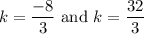
$k=(-8)/(3)\text{ and }k=(32)/(3)$

Therefore, the two points are
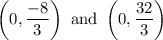$\left(0,(-8)/(3)\right)\text{ and }\left(0,(32)/(3)\right)$ .

Please log in or register to add a comment.