Question

A competitive knitter is knitting a circular place mat. The radius of the mat is given by the formula

363
r(t) = 3 -
with r in centimeters and t in seconds.
(t + 11)
A. Find the rate at which the area of the mat is increasing.
Select an answer
B. Use your expression to find the rate at which the area is expanding at t = 5.
Round your answer to 2 decimal(s).
Select an answer

Answer 1

Answer: A.
`A'(t)=(4356\pi)/((t+11)^(3))-(527076\pi)/((t+11)^(5))`

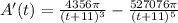
B. A'(5) = 1.76 cm/s

Explanation: Rate of change measures the slope of a curve at a certain instant, therefore, rate is the derivative.

A. Area of a circle is given by

`A=\pi.r^(2)`

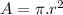
So to find the rate of the area:

`(dA)/(dt)=(dA)/(dr).(dr)/(dt)`

`(dA)/(dr) =2.\pi.r`

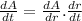
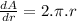
Using
`r(t)=3-(363)/((t+11)^(2))`

`(dr)/(dt)=(726)/((t+11)^(3))`

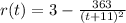
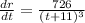
Then

`(dA)/(dt)=2.\pi.r.[(726)/((t+11)^(3))]`

`(dA)/(dt)=2.\pi.[3-(363)/((t+11)^(2))].(726)/((t+11)^(3))`

Multipying and simplifying:

`(dA)/(dt)=(4356\pi)/((t+11)^(3)) -(527076\pi)/((t+11)^(5))`

The rate at which the area is increasing is given by expression
`A'(t)=(4356\pi)/((t+11)^(3)) -(527076\pi)/((t+11)^(5))`.

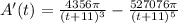B. At t = 5, rate is:

`A'(5)=(4356\pi)/((5+11)^(3)) -(527076\pi)/((5+11)^(5))`

`A'(5)=(4356\pi)/(4096) -(527076\pi)/(1048576)`

`A'(5)=(2408693760\pi)/(4294967296)`

`A'(5)=1.76268`

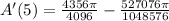
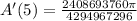
At 5 seconds, the area is expanded at a rate of 1.76 cm/s.