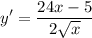Answer:
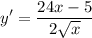
General Formulas and Concepts:
Algebra I
- Exponentials [Fractions] - Are radicals
- Exponential Rule [Rewrite]:
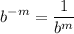
Calculus
Derivatives
Derivative Notation
Derivative of a constant is 0
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Product Rule:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2022/formulas/mathematics/college/c6fshhoq1mws6w0d0la17c7k2dcytwd8kg.png)
Explanation:
Step 1: Define
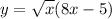
Step 2: Differentiate
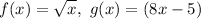
- Product Rule:
![\displaystyle y' = (d)/(dx)[√(x)] \cdot (8x - 5) + √(x) \cdot (d)/(dx)[(8x - 5)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ecf532g2thm134fw2hyjoreqlgr5g7cxmx.png)
- Rewrite:
![\displaystyle y' = (d)/(dx)[x^{(1)/(2)}] \cdot (8x - 5) + √(x) \cdot (d)/(dx)[(8x - 5)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/u0teczhe8cpqz03aomw7yyi54nskvan6xw.png)
- Basic Power Rule:
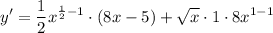
- Simplify:
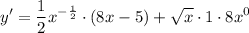
- Rewrite:
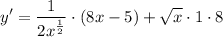
- Multiply:
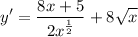
- Rewrite:
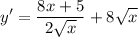
- Add/Rewrite: