Question

An ellipse is defined by 3x2 +2y2 =k and the length of its major axis is 6. What is the value of k?​

Answer 1

Given:

The equation of the ellipse is

`3x^2+2y^2=k`

The length of its major axis is 6.

To find:

The value of k.

Solution:

The standard form of an ellipse is

`(x^2)/(b^2)+(y^2)/(a^2)=1`

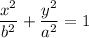
Where, a>b and 3a is the length of major axis.

We have,

`3x^2+2y^2=k`

Divide both sides by k.

`(3x^2+2y^2)/(k)=(k)/(k)`

`(x^2)/((k)/(3))+(y^2)/((k)/(2))=1`

`\frac{x^2}{(\sqrt{(k)/(3)})^2}+\frac{y^2}{(\sqrt{(k)/(2)})^2}=1`

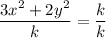
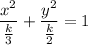
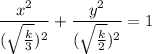
Here,
`\sqrt{(k)/(2)}>\sqrt{(k)/(3)}`.

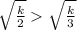So, the length of the major axis is

`2\sqrt{(k)/(2)}=6`

`\sqrt{(k)/(2)}=3`

`(k)/(2)=9`

`k=18`

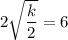
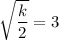
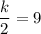
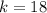
Therefore, the value of k is 18.