Question

Suppose the angle of depression from a race car driver's eyes to the bottom of the 3 foot high back end of the car in front of him is 18 degrees. How far apart, to the nearest foot, are their bumpers? Assume the horizontal distance from the race car driver's eyes to the front of his car is 5 feet

Answer 1

`\Huge \boxed{\boxed{\boxed{\textbf{4 feet}}}}`

Explanation:

To find the distance between the bumpers of the two race cars, we can use the angle of depression and trigonometry. In this case, the angle of depression is 18 degrees, and the vertical distance from the driver's eyes to the bottom of the car in front of him is 3 feet.

We can use the tangent function to solve the problem, as the tangent of an angle in a right triangle is equal to the ratio of the opposite side (perpendicular) to the adjacent side (base).

Let's denote the vertical distance as "y" (3 feet) and the horizontal distance between the bumpers as "x". We have:

`\LARGE \boxed{\boxed{\tt{\tan(18^\circ) = (y)/(x)}}}`

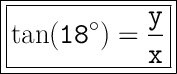
We know that the vertical distance "y" is 3 feet, so we can plug that value into the equation:

`\Large \boxed{\tt{\tan(18^\circ) = (3)/(x)}}`

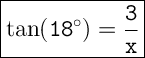
Now, we can solve for "x":

• 
  `\tt{x = (3)/(\tan(18^\circ))}`

• 
  `\tt{x = 9.233050612}`

However, we need to take into account the 5 feet horizontal distance from the race car driver's eyes to the front of his car. So, we subtract that value:

• 
  `\Large \tt{9.233050612 - 5 = 4.233050612}`

Rounding to the nearest foot, the distance between the bumpers of the two race cars is approximately 4 feet.

#BTH1

________________________________________________________